Parabolspiegel für den digitalen Fernsehempfang
Von Klasse 9 bis Klasse 12 nehmen Parabeln einen hohen Stellenwert innerhalb des Mathematikunterrichts ein. Untersucht man Parabeln etwas genauer, können wir uns dank der Mathematik zum Beispiel die Arbeitsweise von Satellitenschüssel erklären, die zu tausenden auf den Berliner Dächern und Balkonen stehen und tagtäglich für einen einwandfreien Fernsehempfang sorgen.
Parabolspiegel für Großanbieter, zum Beispiel von Kabelfernsehen
Jede Satellitenschüssel ist aufgebaut wie ein Parabolspiegel. In einem gewissen Abstand vom Mittelpunkt befindet sich das Empfangsmodul, welches die elektromagnetischen Strahlen, die von den Satelliten ausgestrahlt werden, aufnehmen. Man nennt diese Stelle den Brennpunkt des Parabolspiegels.
Wir wollen nun herausfinden, wie weit vom Mittelpunkt der Parabolbrennpunkt liegt und ob es eine Gesetzmäßigkeit für den Brennpunkt gibt.
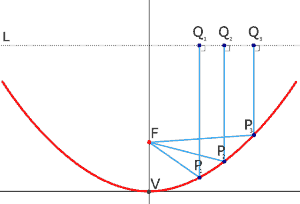
Da der Parabolspiegel vollkommen symmetrisch ist, brauchen wir uns lediglich einen Querschnitt davon anzusehen. Aus dem dreidimensionalen Parabolspiegel ist eine zweidimensionale Parabel entstanden – und die kennen wir ja aus dem Mathematikunterricht.
Der Satellit ist sehr, sehr weit entfernt, daher fallen die elektromagnetischen Strahlen parallel auf bzw. in die Schüssel. Im folgenden Bild sind drei Strahlen in Blau eingezeichnet.
Paralleler Einfall der elektromegnetsichen Strahlen in den Parabolspiegel
Die reflektierten Strahlen bündeln sich alle in einem Punkt, dem Parabelbrennpunkt.
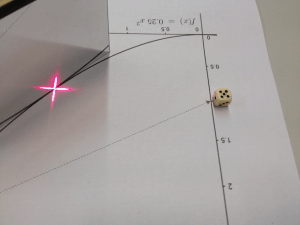
Die Abbildungen zeigen Schülerinnen und Schüler bei dem praktischen Nachweis des Parabelbrennpunktes mithilfe eines Laser-Pointers und eines kleinen Spiegels. Der Spiegel wird tangential an den Graphen der Parabel gestellt und der Laser leuchtet parallel zur Y-Achse. Der Würfel liegt genau auf dem Parabelbrennpunkt – er wird von dem reflektierten Laser-Strahl getroffen!
Die folgende GeoGebra-Animation zeigt uns, dass jede Parabel einen Brennpunkt hat.
Die graue gestrichelte Linie ist die Tangente des Graphen. Du kannst Dir die Tangente als einen kleinen Taschenspiegel vorstellen, den Du ganz dicht an die Kurve hältst.
Aus unserem Billardraum in Haus F (oder alternativ aus dem Physikunterricht) wissen wir, dass für die Strahlen (genauso wie für die Billardkugeln) Einfalls- und Ausfallswinkel gleich sind.
Kommen wir zurück zu unserer Ausgangsfrage: Wo genau liegt der Parabelbrennpunkt?
Tipp:
Schau Dir die Koordinaten des Brennpunktes für a = 1, a = 2, a = 3 und so weiter an.
f(x) = 1·x² --> a = 1 --> F(0|0,25) = F(0|1/4)
f(x) = 2·x² --> a = 2 --> F(0|0,125) = F(0|1/8)
f(x) = 3·x² --> a = 3 --> F(0|0,0833) = F(0|1/12)
f(x) = 4·x² --> a = 4 --> F(0|0,0625) = F(0|1/16)
Auf die allgemeine Regel bist Du sicherlich schon ganz alleine gekommen, oder?
Für die Parabel f(x) = a·x² liegt der Parabelbrennpunkt bei F(0|1/(4·a) ).
Autor: Andreas Fischer, Lehrer für Mathematik und Informatik an der GHO
Klassenstufe: 10 (E- oder F-Kurs) bzw. 11 (Grundkurs)
Quellennachweise:
Die Bilder stammen von den Seiten http://res.cloudinary.com/hxmj4muxr/image/upload/v1/33/2012/10/Satellitenschuessel-digital.jpg und https://en.wikipedia.org/wiki/Parabolic_antenna und wurden jeweils am 3. 6. 2016 abgerufen.
Das GeoGebra-Arbeitsblatt stammt vom Autor.
